
苗兵,博士,教授,博士生导师
Bing Miao, Ph.D., Professor
Email:bmiao AT ucas DOT ac DOT cn
研究领域
研究兴趣:对与(随机/量子,平衡/非平衡)涨落有关的理论物理基础问题有广泛兴趣
专业科普系列:
统计物理
高分子统计物理漫谈,高分子物理和临界现象-n=0 模型,超对称高分子场论-1,
高分子链(自回避行走)的n=0场论表述,高分子自回避行走链 n=0场论的两种推导
界面涨落,界面涨落的曲率效应,界面问题的统计力学,界面问题的估算,界面张力的临界指数
中心极限定理,Fokker-Planck 方程-薛定谔方程,统计物理的变分法 , 对偶 , 高维球面面积,统计场论概要
卡西米尔力,表面力, 零点能的来源, 栗弗席兹理论-1, 长程相互作用与热力学极限, 静电关联能
漫谈熵,玻尔兹曼分布,熵的朗道处理, 广延性与Gibbs-Duhem关系
路径积分: 谐振子能谱, 维克定理的简单推导, 一个路径积分的证明, 谐振子路径积分的涨落因子, 自由涨落, 一个技巧, 路径积分到热核及zeta函数
Gelfand-Yaglom 定理, 一个泛函行列式的有益讨论, 雅克比场与泛函行列式, 路径积分系列(Topics on Path Integrals)
自洽平均场方程, 自回避行走的标度讨论, 高斯D-流形上的关联, 聚合物链的伊藤写法, 半刚性链的伊藤写法
软物质物理: 高分子溶液散射函数, 德拜-休克尔屏蔽, 高分子溶液的关联效应, 屏蔽效应, 极小曲面
统计物理短评集-1, 统计物理短评集-对偶空间, 统计物理短评集-3, 统计物理短评集-4
非平衡统计物理系列:
涨落耗散-线性响应,涨落耗散定理-2, 涨落耗散定理-3, 涨落耗散定理-4, 涨落耗散定理-5, 从因果性到色散关系, 量子涨落耗散定理
伊藤清的公式,伊藤-郎之万方程, Fokker-Planck 方程:伊藤方法, 薛定谔方程的随机涨落视角, 随机涨落系列, 福克-普朗克方程的解
从爱因斯坦关系到李雅普诺夫方程, 爱因斯坦关系的另一种推导, Martin-Siggia-Rose场论方法, 李雅普诺夫方程
大数定律和中心极限定理, 大偏差理论: 压缩原理(Contraction Principle), 最大熵分布-1, 最大熵分布-2
Jarzynski等式的一个证明, 平衡态涨落耗散定理的结构, 随机热力学二定律(Intro to Stochastic Thermodynamics)
数学物理方法
解析函数,漫谈-几乎浪漫,傅里叶级数是洛朗级数,The Argument Principle,柯西定理,代数基本定理, 解析, 调和函数的平均值性质
狄拉克博士的怪函数-1, 狄拉克博士的怪函数-2,由傅里叶变换算高斯积分, 复参数高斯积分, 狄拉克梳, 拉普拉斯算子的格林函数
古典微分几何速写, 测地线方程, 从偏导到变分, 特殊函数怎么来, 狄拉克的技巧, 朗道的妙着, 费曼技巧, 巧算高斯积分
从傅里叶变换到梅林变换, 参数变易法与格林函数法, 参数变易法: 福克-普朗克算子的厄米化
黎曼猜想系列:
绝妙的证明 , 绝妙的证明-2, 从阶乘说开去 , 黎曼 zeta 函数, 黎曼 zeta 函数的值, 傅里叶级数方法, zeta 函数与泛函行列式
黎曼博士的函数, 一个证明, 一个 zeta(2m) 的新推导, 一个美妙的函数关系, 拉马努金式游戏, 黎曼 zeta 函数的留数
数学物理随笔:
驯服发散, 鞍点近似法, 由狄拉克梳证明 Delta 函数的积分表示, 简易拉普拉斯变换, Polygamma 函数
报告视频:
A New Information Thermodynamics
Casimir Force and Path Integral for Higher Derivative Actions
Casimir Force in Statistical Physics
Thermal Casimir Forces for Higher Derivative Actions
Casimir Forces for Higher Derivative Actions
Fluctuation Theory in Polymer Physics
Phase Separation Theory of Polyelectrolyte Solution
讲课视频:
数学物理方法:微分算符的曲线坐标表示
界面的统计热力学:界面动力学与瑞利-普拉托不稳定性,浸润与液滴形状
1. 高分子物理
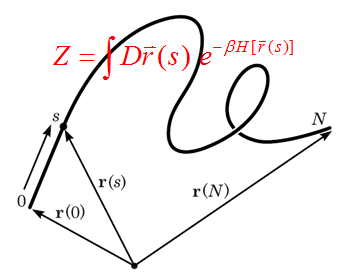
(A) 理论综述
高分子统计场论方法参考: On the Structure of Statistical Field Theory of Polymers
高分子物理中的路径积分和标度理论参考: Polymer Theory: Path Integrals and Scaling
高分子物理中的几何与拓扑问题参考: Some Geometrical and Topological Problems in Polymer Physics
高分子物理场论方法综述:Field theoretic approach for block copolymer melts: SCFT and FTS
(B) 涨落理论
受限空间中的高斯涨落理论参考:Effects of Confinements on the Order-Disorder Transition of Diblock Copolymer Melts
单圈重整化涨落理论参考:Fluctuation Effects and the Stability of the Fddd Network Phase in Diblock Copolymer Melts
2. 卡西米尔物理
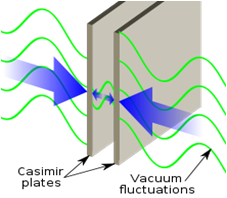
卡西米尔力参考:
Materials Perspective on Casimir and van der Waals Interactions
Collective Behavior of Colloids due to Critical Casimir Interactions
3. 生物物理
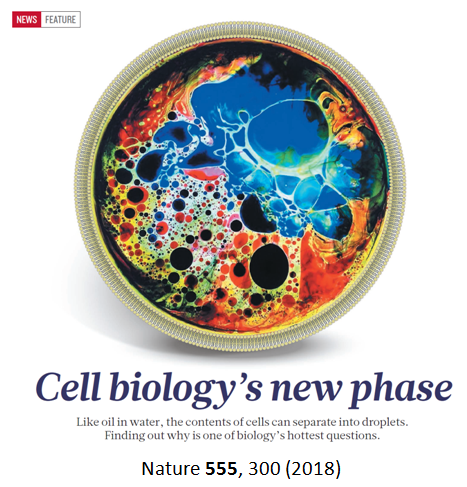
细胞内相变参考:
Polymer Physics of Intracellular Phase Transitions
Liquid-Liquid Phase Separation in Biology
Protein Phase Separation: A New Phase in Cell Biology
我们在 Kavli 理论科学研究所 (Kavli-ITS) 组织的软物质-非平衡涨落 Workshop:
Soft Matter Out of Equilibrium: from driven to active systems (May 19 - 25, 2019, Beijing)

招生信息
招生专业:070201 - 理论物理
学习和工作经历
2006年博士毕业于中国科学院。2006年-2011年先后在加拿大圣弗朗西斯泽维尔大学和圭尔夫大学物理系,德国马普高分子研究所理论系做博士后。2011年起在中国科学院大学任教至今。2019年3月和9月分别任德国马普智能体系研究所和法国波尔多大学理论物理组访问教授。现任兰州大学物理学院兼职教授。
讲授课程
数学物理方法、统计热力学、软凝聚态理论等。
论文书籍
书籍
1. 《高分子物理理论专题》,严大东,张兴华,苗兵,科学出版社 (2021).
代表论文
统计力学基础/路径积分/随机动力学/高阶场论/卡西米尔力
1. "Emergence of Newtonian Deterministic Causality from Stochastic Motions in Continuous Space and Time", Bing Miao, Hong Qian, Yong-Shi Wu, arXiv:2406.02405
2. "Correlation decoupling of Casimir interaction in an electrolyte driven by external electric fields", Guangle Du, David S. Dean, Bing Miao, Rudolf Podgornik, Phys. Rev. Lett. 133, 238002 (2024); arXiv:2404.06028
3. "On Thermodynamic Information", Bing Miao, Hong Qian, Yong-Shi Wu, arXiv:2312.03454
4. "Path Integrals for higher derivative actions", David S. Dean, Bing Miao, Rudolf Podgornik, J. Phys. A: Math. Theor. 52 505003 (2019); arXiv: 1906.08626
5. "Thermal Casimir interactions for higher derivative field Lagrangians: generalized Brazovskii models", David S. Dean, Bing Miao, Rudolf Podgornik, J. Phys. A: Math. Theor. 53 355005 (2020); arXiv:2002.09822
6. "Casimir force", Bing Miao, Acta Physica Sinica, 69 (8), 080505 (2020). Invited.
聚电解质物理
1. "Size Effect of Multivalent Counterions on Polyelectrolyte Brushes in Different Polar Solvents", Hong-Ge Tan, Li-De Guo, Han-Yang Qian, Li-Xiang Liu, Qing-Hai Hao, Bing Miao, Macromolecules 56 (23), 9312 (2023).
2. "Surface Morphologies of Planar Ring Polyelectrolyte Brushes induced by Trivalent Salts", Qing-Hai Hao, Jie Cheng, Li-Xiang Liu, Hong-Ge Tan, Tong Wei, Li-Yan Liu, Bing Miao, Macromolecules 53 (16), 7187 (2020).
3. "Morphological Response of a Spherical Polyelectrolyte Brush to Solvent Quality and Electrostatic Interaction Strength", Qing-Hai Hao, Gang Xia, Bing Miao, Hong-Ge Tan, Xiao-Hui Niu, Li-Yan Liu, Macromolecules, 51, 8513 (2018).
4. "Confinement Effects on Phase Separation of a Polyelectrolyte Solution", Jie Fu, Bing Miao, Dadong Yan, Polymer, 110, 49 (2017). Feng Xinde Polymer Prize (The Best Paper Nomination).
5. "Curvature elasticity of a grafted polyelectrolyte brush", Zhen Lei, Bing Miao, Shuang Yang, Er-Qiang Chen, Phys. Rev. E, 91, 062602 (2015).
6. "Configurational fluctuation effects on counterion condensation for a polyelectrolyte chain", Bing Miao, Thomas A. Vilgis, Macromol. Theory Simul., 21, 582 (2012).
界面物理
1. "Nonequilibrium Dynamic Phase Diagram for Transmembrane Transport of Active Particles", Haixiao Wan, Duo Xu, Wei Wang, Yanfang Cheng, Xiaobin Dai, Xueqing Jin, Lijuan Gao, Xuanyu Zhang, Bing Miao, Qiang He, Li-Tang Yan, ACS Nano, 18, 24024 (2024).
2. "Polymeric Microparticles Generated via Confinement-Free Fluid Instability", Jianing Song, Wenluan Zhang, Dehui Wang, Yue Fan, Chenglin Zhang, Dapeng Wang, Longquan Chen, Bing Miao, Jiaxi Cui, Xu Deng, Advanced Materials, 33, 2007154 (2021).
3. "How Implementation of Entropy in Driving Structural Ordering of Nanoparticles Relates to Assembly Kinetics: Insight into Reaction-Induced Interfacial Assembly of Janus Nanoparticles", Ye Yang, Pengyu Chen, Yufei Cao, Zihan Huang, Guolong Zhu, Ziyang Xu, Xiaobin Dai, Shi Chen, Bing Miao, Li-Tang Yan, Langmuir, 34, 9477 (2018).
4. "Diffusion and Directionality of Charged Nanoparticles on Lipid Bilayer Membrane", Pengyu Chen, Zihan Huang, Junshi Liang, Tianqi Cui, Xinghua Zhang, Bing Miao, Li-Tang Yan, ACS Nano, 10 (12), 11541 (2016).
5. "Scaling of Polymer Dynamics at an Oil–Water Interface in Regimes Dominated by Viscous Drag and Desorption-Mediated Flights", Dapeng Wang, Renfeng Hu, Joshua N. Mabry, Bing Miao, David T. Wu, Kaloian Koynov, Daniel K. Schwartz, J. Am. Chem. Soc., 137 (38), 12312 (2015).
高分子链统计力学/结构因子/非高斯链
1. "Optimal Reactivity and Improved Self-Healing Capability of Structurally-Dynamic Polymers Grafted on Janus Nanoparticles Governed by Chain Stiffness and Spatial Organization", Guoxi Xu, Zihan Huang, Pengyu Chen, Tianqi Cui, Xinghua Zhang, Bing Miao, Li-Tang Yan, Small, 13, 1603155 (2017). Front Cover
2. "Microphase separation of short wormlike diblock copolymers with a finite interaction range", Ying Jiang, Xinghua Zhang, Bing Miao, Dadong Yan, Jeff Z. Y. Chen, Soft Matter, 12, 2481 (2016).
3. “Structure factor of a Gaussian chain confined between two parallel plates”, Yi Liao, Bing Miao, J. Chem. Phys., 142, 164903 (2015).
4. "The structure factor of a wormlike chain and the random-phase-approximation solution for the spinodal line of a diblock copolymer melt", Xinghua Zhang, Ying Jiang, Bing Miao, Yunlin Chen, Dadong Yan, Jeff Z. Y. Chen, Soft Matter, 10 (29), 5405 (2014).
5. “Effect of finite-extensibility on the equilibrium chain size”, Bing Miao, Thomas A. Vilgis, Stefanie Poggendorf, Gabriele Sadowski, Macromol. Theory Simul., 19, 414 (2010).
相变理论/重正化场论
1. "On the structure of statistical field theory of polymers", Bing Miao, Int. J. Mod. Phys. B, 27, 1361009(2013).
2. “Fluctuation effects and the stability of the Fddd network phase in diblock copolymer melts”, Bing Miao, Robert A. Wickham, J. Chem. Phys., 128, 054902 (2008). Selected at Virtual Journal of Nanoscale Science & Technology, Volume 17, Issue 7 (2008).
3. “The nature of phase transitions of symmetric diblock copolymer melts under confinement”, Bing Miao, Dadong Yan, Robert A. Wickham, An-Chang Shi, Polymer, 48, 4278 (2007).
4. “Effects of confinement on the order-disorder transition in diblock copolymer melts”, Bing Miao, Dadong Yan, Charles C. Han, An-Chang Shi, J. Chem. Phys., 124, 144902 (2006). ; Selected at Virtual Journal of Nanoscale Science & Technology, Volume 13, Issue 16 (2006).
5. “Conformation-assisted fluctuation of density and kinetics of nucleation in polymer melts”, Hongge Tan, Bing Miao, Dadong Yan, J. Chem. Phys., 119, 2886 (2003).
学术交流
2023. 08, 兰州理论物理中心。
2022. 10, 清华大学化工系软物质理论与模拟组。
2021. 01, 兰州理论物理中心。
2020. 05, 天津大学量子交叉研究中心。
2019. 10, 北京师范大学系统科学学院。
2019. 09, 法国波尔多大学 LOMA 理论物理组。
2019. 08, 兰州大学物理系。
2019. 03, 德国马普智能体系研究所理论物理组访问科学家。
2019. 01, 中科院理论物理所彭桓武理论物理青年科学家论坛。
2019. 01, 大理大学统计物理研讨会。
2018. 12, 东华大学先进低维材料中心。
2018. 11, 电子科大基础与前沿研究院。
2018. 08, 上海交通大学自然科学研究院。
2018. 04, 北京航空航天大学软物质研究中心。
2018. 04, 苏州大学软凝聚态物理中心。
2017. 11, 清华大学化工系。
2015. 07, 德国马普高分子研究所。
2012. 12, 以色列特拉维夫大学物理系。
2012. 08, 清华大学周培源应用数学中心。
2011. 06, 中国科技大学高分子科学系。
2009. 07, Les Houches Physics Summer School, France.
邀请报告
45. Path Integrals for Higher Derivative Actions, 2023. 11, 第十二届复杂体系计算统计力学研讨会,华南师范大学,广州。
44. Fluctuation and Effective Force, 2023. 10, 热化与涨落关系国际研讨会,厦门大学。
43. Functional Determinant in 1D Field Theory, 2023. 05, 第七届量子信息、时空及拓扑物质国际会议,山西大同大学。
42. Path Integral and Casimir Force for Higher Derivative Actions, 2022. 10, 北京雁栖湖应用数学研究院 (BIMSA), 北京。
41. Thermal Casimir Force for Higher Derivative Actions, 2022. 08, 第十五届亚洲太平洋地区物理学术会议 (APPC15),韩国。
40. Casimir Force in Statistical Physics, 2022. 08, 宁夏大学物理学院。
39. Casimir Force and Path Integral, 2021. 08, 第六届全国统计物理与复杂系统学术会议,长春,吉林大学。
38. Thermal Casimir Force, 2021. 07, 第八届软凝聚态物理研讨会,上海交大自然科学研究院。
37. Casimir Force in Statistical Physics, 2021. 06, 东华大学低维中心。
36. Orders and Interactions in Polyelectrolyte Systems, 2021. 06, 第十三届国际聚电解质大会,华东理工大学。
35. Casimir Force and Path Integral for Higher Derivative Actions, 2021. 05,第六届量子信息、时空及拓扑物质国际会议,重庆大学。
34. Fluctuation Theory in Polymer Physics,2021. 04,杭师大材化学院高分子物理学术交流。
33. Casimir Force in Statistical Physics,2021. 04,西北师大理论物理交流平台。
32. Fluctuation Theory in Polymer Physics,2020. 10,中科院理论物理研究所。
31. Casimir Force in Statistical Physics,2020. 08,计算物理与复杂系统研讨会,兰州大学。
30. Casimir Force in Statistical Physics,2020. 06,中物院研究生院学术讲座。
29. Casimir Forces for Higher Derivative Actions,2020. 05,天津大学量子交叉中心凝聚态物理前沿讲座。
28. Theory of Phase Separations in Polyelectrolyte Systems,2019. 12,太平洋高分子学术会议,新加坡。
27. Casimir Forces and Path Integrals for Higher Derivative Actions,2019. 10,北师大系统科学学院。
26. Fluctuation-related physics of polymers,2019. 10,全国高分子学术论文报告会,西安。
25. Thermal Casimir Forces within Gaussian Field Theory,2019. 08,兰州大学理论物理交流平台。
24. Recent Progress on Casimir Physics,2019. 08,北航软物质物理研究中心。
23. Casimir Forces in Gaussian Fluctuating Media,2019. 07,第五届全国统计物理与复杂系统学术会议,合肥,中国科技大学。
22. Phase Separations of Polyelectrolytes,2019. 07,第十五届中韩双边高分子材料研讨会,恩施。
21. Casimir Forces in Ising and Brazovskii Fluctuation Media within a Gaussian Model,2019. 06,弗里德曼引力和宇宙学及卡西米尔效应研讨会,圣彼得堡,俄罗斯。
20. Casimir Forces in Gaussian Fluctuating Media,2019. 06,国家天元数学东北中心,长春,吉林大学。
19. Fluctuations in Polymer Physics,2019. 03,德国马普智能体系研究所理论物理组,斯图加特。
18. Phase Separations in Polyelectrolyte Systems,2018. 11,国际软物质科学与工程研讨会,成都,四川大学。
17. Phase Separations in Polyelectrolyte Systems,2018. 10,国际高分子科学研讨会,北京大学软物质研究中心。
16. 聚电解质溶液相分离理论,2018. 09,中国物理学会秋季会议,大连理工大学。
15. 高分子统计物理,2018. 08,江苏科技大学材料学院。
14. Field Theory of Polymers, 2018. 06, 广州大学智能制造工程研究院。
13. 关联函数,2018. 04,北航软物质物理研究中心。
12. Theoretical Study on Phase Transitions in Polymers,2018. 04,苏州大学软凝聚态物理中心。
11. 高分子体系的有序和涨落, 2017. 11,清华大学化工系。
10. EMN Meeting on Polymer 2016, 2016/01/12-2016/01/15, Hong Kong.
9. Phase separations in polyelectroyte solutions: effect of chain flexibility, at the Soft Matter Workshop, Kavli Institute for Theoretical Physics China, August, 2015.
8. Phase separations in polyelectroyte solutions: effect of chain rigidity, at the Theory Group, Max Planck Institute for Polymer Research, July, 2015.
7. Pole distribution and structuring in a polymer system, at the Beijing University of Chemical Technology, July, 2014.
6. The poles of scattering function and the structuring for a polymer system, at the Seminar of Theory and Simulation in Macromolecular Systems, Changchun Institute of Applied Chemistry, CAS, June, 2014.
5. Microphase separation under confinement: A field-theoretic study, at the Fritz Haber Center, Hebrew University of Jerusalem, December, 2012.
4. Some field theoretic methods in polymer physics, at the Zhou Pei-Yuan Center for Applied Mathematics, Tsinghua University, August, 2012.
3. Some progresses on the study of phase behavior in polyelectrolyte solutions, at the Seminar of Theory and Simulation in Macromolecular Systems, Nanjing University, May, 2012.
2. Theoretical methods in polymer physics, Series Lectures at the Soft Matter Group, University of Science and Technology of China, June, 2011.
1. Theoretical study on structure phase transitions in polymer systems, at the Seminar of Advanced Polymer Materials, Qingdao University of Science and Technology, April, 2011.
会议报告
5. “Field-theoretic methods in polymer physics”, Bing Miao, the 17th Conference for Condensed Matter Theory and Statistical Physics, Lanzhou, 2012.
4. “Effect of finite-extensibility on the equilibrium chain size”, Bing Miao, Thomas A. Vilgis, Stefanie Poggendorf, and Gabriele Sadowski, DPG Spring Meeting, Regensburg, 2010.
3. “Morphologies of a diblock copolymer melt confined in a spherical nanopore”, Bing Miao, Janine Tulkens, Weihua Li, and Robert A. Wickham, International Symposium on Polymer Physics, Xiamen, 2008.
2. “Morphologies of a diblock copolymer melt confined in a spherical nanopore”, Bing Miao, Janine Tulkens, Weihua Li, and Robert A. Wickham, APS March Meeting, New Orleans, 2008.
1. “Fluctuation effects and stability of the Fddd network phase in diblcock copolymer melts”, Bing Miao and Robert A. Wickham, APS March Meeting, Denver, 2007.
相册
With Leticia and Jorge, at Hangzhou, 2024. 08.

With Hong, at Beijing, 2024. 08.

With David and Rudi, at Beijing, 2024. 04.

Conference on Active Matter, 2024. 01, Wenzhou.

Workshop on Thermalization and Fluctuation Relatioins, 2023. 10, Xiamen Univ.

With Hong, at Beijing, 2023. 08.

With David, at Bordeaux, France.


Bordeaux, France.

With David, at Mutianyu Great Wall, Beijing.

With Rudi, St. Petersburg, 2019. 06.

St. Petersburg, 2019. 06.


The Fourth Symposium on Casimir Effect, 2019. 06, St. Petersburg.

Group Photo of Kavli-ITS workshop on non-Equilibrium fluctuations, 2019. 05, Beijing.

With Rudi and David, 2019. 05, Qingdao.

With Rudi and David, 2019. 03, Huairou.

Schloss Ringberg Conference, Max Planck Society, 2019, 03, Bavarian Alps.

With MPI-IS Theoretical Physics Group, 2019. 03, Stuttgart.

Polyelectrolyte Symposium at Donghua University, 2018. 12, Shanghai.

With J. Zinn-Justin during his series lectures on RG, 2017. 11, ITP-Cas, Beijing.

MPI-P


Les Houches School of Theoretical Physics, 2009. 07, France.





